알고리즘 - 플로이드 와샬 알고리즘(Floyd Warshall Algorithm)

* 참고 저서 <이것이 취업을 위한 코딩테스트다> 나동빈저

 

 https://gae-gi-da.tistory.com/entry/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-%EB%8B%A4%EC%9D%B5%EC%8A%A4%ED%8A%B8%EB%9D%BC-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98Dijkstra

알고리즘 - 다익스트라 알고리즘(Dijkstra)

다익스트라 알고리즘이 하나의 시작 지점에 대해 각 노드까지의 최단 거리를 구하는 것이었다면,

플로이드 와샬 알고리즘은 모든 노드에 대해서 모든 노드까지의 최단 경로를 구하는 것이다.

 

1,2,3,4의 노드와 그 사이 간선들이 있다고 가정하자.

플로이드 와샬 알고리즘이 사용하는 테이블은

각 노드마다 각 노드로의 최단 경로를 저장해야 하기에

그 크기는 당연히 n^2이 된다.

 

다음과 같은 테이블이 생기게 된다

 

 

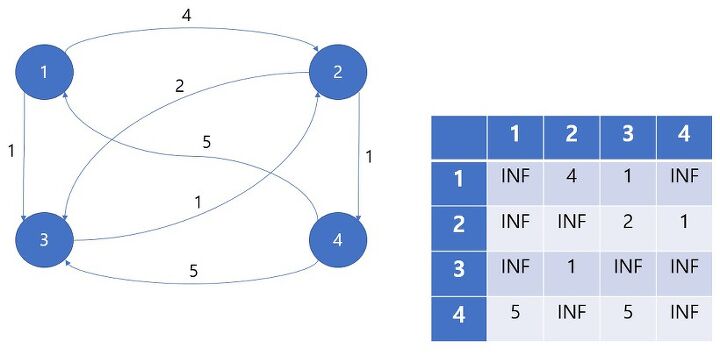
이 테이블들은 마치 다익스트라 알고리즘처럼 단계마다 갱신해주게 되는데,

각 단계는 '노드 n을 거쳤을 때'가 된다.

 

표를 통해 다시 설명하자면

1 -> 1	1 -> 2	1 -> 3	1 -> 4
2 -> 1	2 -> 2	2 -> 3	2 -> 4
3 -> 1	3 -> 2	3 -> 3	3 -> 4
4 -> 1	4 -> 2	4 -> 3	4 -> 4

다음과 같은 n^2 만큼의 테이블이 생성되고 각 값은

'n번 노드' -> 'm번 노드' 까지의 최단 경로를 저장하고 있다.

 

1 -> 2 칸에 대한 변화만 살펴본다면

가장 처음엔 1번 노드서 2번 노드로 향하는 간선이 있다면

그 가중치가 저장되고, 없을 경우 inf(무한대) 가 저장될 것이다.

 

이후에는 반복문 내에서

n,m을 제외한 노드 k들에 대해서 k를 거쳐 n에서 m으로 갈 때의 거리와 비교하여

그 중 적은 값을 저장한다.

이를 점화식으로 나타내자면 Dnm = min(Dnm, Dnk + Dkm)와 같을 것이다.

 

반복이 끝나면 테이블의 각 값들은 n에서 m으로 가는 최종적인 최단 경로를 값으로 지니게 된다.

 

수행시간의 경우 v^2제곱만큼의 값들에 대해 각각 n번의 비교 연산을 수행하기에

O(v^3)의 수행시간을 가지게 된다

 

세제곱의 수행시간은 상당히 큰 수행시간이며, 보통 현실적인 시간 내에 해결할 수 없는 알고리즘으로 분류된다.

대신 코드가 간단하고 모든 값을 구할 수 있다는 장점이 있다.

입력의 크기가 한정적인 문제들에 대해서만 사용할 수 있을 거라 생각되기에,

알고리즘 문제의 입력 크기를 잘 살펴보고 적절히 사용할 필요가 있어 보인다.

 

코드는 다음과 같다.

INF = int(le9)

n = int(input())
m = int(input())

graph = [[INF]*(n+1) for _ in range(n+1)]

for a in range(1, n+1):
	for b in range(1, n+1):
    	if a == b:
        	graph[a][b] = 0
            
 for _ in range(m):
 	a,b,c = map(int,input().split())
    graph[a][b] = c
    
 for k in range(1,n+1):
 	for a in range(1,n+1):
    	for b in range(1,n+1):
        	graph[a][b] = min(graph[a][b],graph[a][k]+graph[k][b])
            
 print(graph)